Working with MPAS Grids#

This notebook showcases how to work with datasets from the Model for Prediction Across Scales (MPAS).

MPAS Grid Overview#

The defining feature of MPAS when compared to other models is that its unstructured grid is composed of Voronoi Meshes with a C-grid staggering. This means that the grid can be broken down into two meshes: Primal and Dual. The Primal Mesh is composed of Voronoi regions and the Dual Mesh is composed of Delaunay Triangles. The figure below showcases this relationship, with the dashed triangles being the dual of the Voronoi mesh.

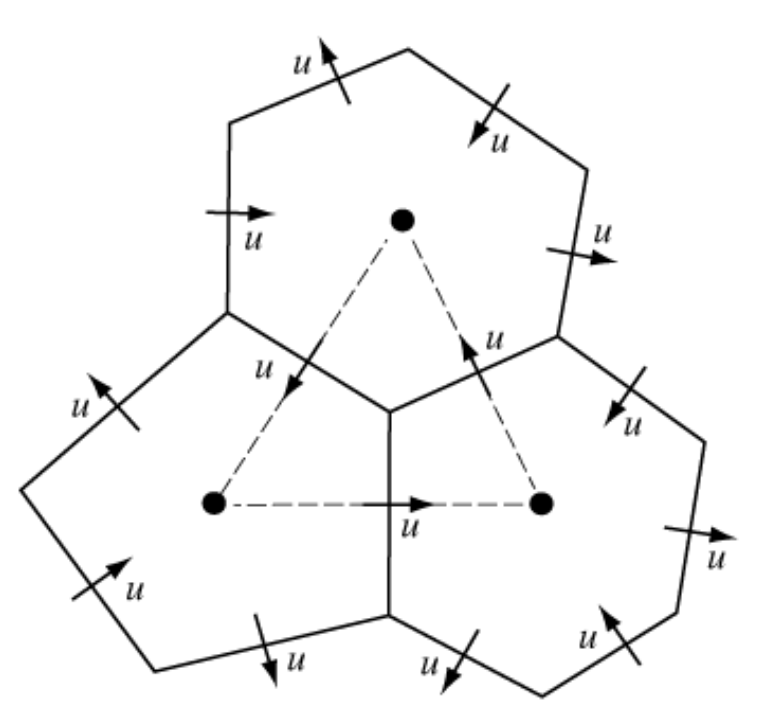
Since the Primal Mesh is predominantly made up of hexagons, with pentagons and heptagons occasionally being present, and the Dual Mesh being strictly triangular, this notebook will showcase how we can represent both of these meshes in the UGRID conventions using UXarray.

Constructing a Grid Object#

Note

Since we only have a Grid file and no Data file in this example, we will be working exclusively with the Grid class to investigate the grid topology and not with UxDataset or UxDataArray data structures.

The xarray.Dataset that we opened in the previous section stores the coordinates and connectivity variables according to the MPAS specification standards for both the Primal and Dual meshes together in a single dataset. Here, instead of opening up the dataset using Xarray, we can pass through the path into our open_grid method to construct an instance of a Grid class. This Grid can take in a use_dual parameter to select whether to construct the Primal or Dual mesh, parsing and encoding the appropriate variables in the UGRID conventions.

import uxarray as ux

primal_mesh = ux.open_grid(mpas_dataset_filepath, use_dual=False)
dual_mesh = ux.open_grid(mpas_dataset_filepath, use_dual=True)

primal_mesh

<uxarray.Grid>
Original Grid Type: MPAS
Grid Dimensions:
  * n_node: 320
  * n_edge: 480
  * n_face: 162
  * n_max_face_nodes: 6
  * n_max_face_edges: 6
  * n_max_node_faces: 3
  * two: 2
  * n_nodes_per_face: (162,)
Grid Coordinates (Spherical):
  * node_lon: (320,)
  * node_lat: (320,)
  * edge_lon: (480,)
  * edge_lat: (480,)
  * face_lon: (162,)
  * face_lat: (162,)
Grid Coordinates (Cartesian):
  * node_x: (320,)
  * node_y: (320,)
  * node_z: (320,)
  * edge_x: (480,)
  * edge_y: (480,)
  * edge_z: (480,)
  * face_x: (162,)
  * face_y: (162,)
  * face_z: (162,)
Grid Connectivity Variables:
  * face_node_connectivity: (162, 6)
  * face_edge_connectivity: (162, 6)
  * edge_node_connectivity: (480, 2)
  * edge_face_connectivity: (480, 2)
  * node_face_connectivity: (320, 3)
Grid Descriptor Variables:
  * edge_face_distances: (480,)
  * edge_node_distances: (480,)

dual_mesh

<uxarray.Grid>
Original Grid Type: MPAS
Grid Dimensions:
  * n_node: 162
  * n_edge: 480
  * n_face: 320
  * n_max_face_nodes: 3
  * n_max_face_edges: 3
  * n_max_node_faces: 6
  * two: 2
  * n_nodes_per_face: (320,)
Grid Coordinates (Spherical):
  * node_lon: (162,)
  * node_lat: (162,)
  * edge_lon: (480,)
  * edge_lat: (480,)
  * face_lon: (320,)
  * face_lat: (320,)
Grid Coordinates (Cartesian):
  * node_x: (162,)
  * node_y: (162,)
  * node_z: (162,)
  * edge_x: (480,)
  * edge_y: (480,)
  * edge_z: (480,)
  * face_x: (320,)
  * face_y: (320,)
  * face_z: (320,)
Grid Connectivity Variables:
  * face_node_connectivity: (320, 3)
  * face_edge_connectivity: (320, 3)
  * edge_node_connectivity: (480, 2)
  * edge_face_connectivity: (480, 2)
  * node_face_connectivity: (162, 6)
Grid Descriptor Variables:
  * edge_face_distances: (480,)
  * edge_node_distances: (480,)

Relationship between MPAS and UGRID#

In the previous two sections, we outlined the set of grid variables used to describe the Primal and Dual meshes and how to open an MPAS grid in UXarray. Here, we provide an overview of how we represent both meshes in the UGRID conventions and how the original grid variables were modified to meet these conventions.

Grid Variables (Primal Mesh)#

node_lon & node_lat

Longitude and Latitude coordinates of the Primal Mesh corner nodes
Derived from lonVertex & latVertex
Converted from Radians to Degrees

face_lon & face_lat

Longitude and Latitude coordinates of the Primal Mesh center nodes
Derived from lonCell & latCell
Converted from Radians to Degrees

face_node_connectivity

Connectivity array describing which nodes make up a face
Derived from verticesOnCell
Padding is replaced with INT_FILL_VALUE
Missing Values (zeros) replaced with INT_FILL_VALUE
Converted to zero-index

edge_node_connectivity

Connectivity array describing which nodes link to form each edge
Derived from verticesOnEdge
Padding is replaced with INT_FILL_VALUE
Missing Values (zeros) replaced with INT_FILL_VALUE
Converted to zero-index

Grid Variables (Dual Mesh)#

node_lon & node_lat

Longitude and Latitude coordinates of the Dual Mesh vertices
Derived from lonCell & latCell, the centers of the Primal Mesh
Converted from Radians to Degrees

face_lon & face_lat

Longitude and Latitude coordinates of the Dual Mesh centers
Derived from lonVertex & latVertex, the vertices of the Primal Mesh
Converted from Radians to Degrees

face_node_connectivity

Connectivity array describing which nodes make up a face
Derived from verticesOnCell
Padding is replaced with INT_FILL_VALUE
Missing Values (zeros) replaced with INT_FILL_VALUE
Converted to zero-index

edge_node_connectivity

Connectivity array describing which nodes link to form each edge
Derived from verticesOnEdge
Padding is replaced with INT_FILL_VALUE
Missing Values (zeros) replaced with INT_FILL_VALUE
Converted to zero-index

References#

[1] https://mpas-dev.github.io/

[2] https://mpas-dev.github.io/files/documents/MPAS-MeshSpec.pdf

[3] http://ugrid-conventions.github.io/ugrid-conventions/

Working with MPAS Grids

Contents

Working with MPAS Grids#

MPAS Grid Overview#

Dataset Overview#

Primal Mesh#

Dual Mesh#

Constructing a Grid Object#

Relationship between MPAS and UGRID#

Grid Variables (Primal Mesh)#

Grid Variables (Dual Mesh)#

Functionality#

Face Area Calculation#

References#